Определение центра тяжести твердого тела неправильной формы. Способы определения координат центра тяжести
Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки

Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела γ , вес элементарной частицы тела
P k = γΔV k (P = γV ) подставить в формулу для определения r C , имеем
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)


Рисунок 1.7
Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии . Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение . Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S 1 и S 2 (S = S 1 + S 2 ). Центры тяжести этих фигур находятся в точках C 1 (x 1 , y 1 ) и C 2 (x 2 , y 2 ) . Тогда координаты центра тяжести тела равны


Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):


Рисунок 1.9
Центры тяжести простейших фигур

Рисунок 1.10
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB , CM = (1/3)AM .
2 Дуга окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. y C = 0 .

dl – элемент дуги, dl = Rdφ , R – радиус окружности, x = Rcosφ , L = 2αR ,
Следовательно:
x C = R(sinα/α) .
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox , на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R .
Центр тяжести сектора совпадает с центром тяжести дуги AB :

14. Способы задания движения точки.
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t . Чтобы записать ее уравнение в явной форме, надо исключить из них t .
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.
15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени Δt :
![]()
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени


Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
Лекция 4. Центр тяжести.
В данной лекции рассматриваются следующие вопросы
1. Центр тяжести твердого тела.
2. Координаты центров тяжести неоднородных тел.
3. Координаты центров тяжести однородных тел.
4. Способы определения координат центров тяжести.
5. Центры тяжести некоторых однородных тел.
Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».
Приведение параллельных сил.
После того как было рассмотрено приведение к центру плоской системы и произвольной пространственной системы сил, мы опять возвращаемся к рассмотрению частного случая системы параллельных сил.
Приведение двух параллельных сил.
В ходе рассмотрения такой системы сил возможны три следующих случая приведения.
1. Система двух коллинеарных сил. Рассмотрим систему двух параллельных и направленных в одну сторону сил P и Q , приложенных в точках А и В . Будем считать, что силы перпендикулярны к этому отрезку (рис.1,а ).
С , принадлежащую отрезку АВ и удовлетворяющую условию:
АС /СВ = Q /P .(1)
Главный вектор системы R C = P + Q по модулюравен сумме этих сил:R C = P + Q .
С с учетом (1) равен нулю: M C = P ∙ АС - Q ∙ СВ = 0.
Таким образом, в результате приведения мы получили: R C ≠ 0, M C = 0. Это означает, что главный вектор эквивалентен равнодействующей, проходящей через центр приведения, то есть:
Равнодействующая коллинеарных сил равна по модулю их сумме, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внутренним образом.
Отметим, что положение точки С не изменится, если силы Р и Q повернуть на угол α . Точка С , обладающая таким свойством называется центром параллельных сил .
2. Система двух антиколлинеарных и не равных по модулю сил. Пусть силы P и Q , приложенные в точках А и В , параллельны, направлены в противоположные стороны и по модулю не равны (рис.1,б ).
Выберем в качестве центра приведения точку С , удовлетворяющую по-прежнему соотношению (1) и лежащую на той же прямой, но за пределами отрезка АВ .
Главный вектор этой системыR C = P + Q по модулю теперь будет равен разности модулей векторов:R C = Q - P .
Главный момент относительно центра С по-прежнему равен нулю: M C = P ∙ АС - Q ∙ СВ = 0, поэтому
Равнодействующая антиколлинеарных и не равных по модулю сил равна их разности, направлена в сторону большей силы, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внешнимобразом.
Рис.1
3. Система двух антиколлинеарных и равных по модулю сил. Возьмем за исходный предыдущий случай приведения. Зафиксируем силу Р , а силу Q устремим по модулю к силеР .
Тогда при Q → Р в формуле (1) отношение АС /СВ → 1. Это означает, чтоАС → СВ , то есть расстояние АС →∞ .
При этом модуль главного вектора R C → 0, а модуль главного момента не зависит от положения центра приведения и остается равным первоначальному значению:
M C = P ∙ АС - Q ∙ СВ = P ∙ ( АС - СВ ) = P ∙ А B .
Итак, в пределе мы получили систему сил, для которой R C = 0, M C ≠ 0, а центр приведения удален в бесконечность, которую нельзя заменить равнодействующей. В этой системе нетрудно узнать пару сил, поэтому пара сил равнодействующей не имеет .
Центр системыпараллельных сил.
Рассмотрим систему n сил P i , приложенных в точках A i (x i , y i , z i )и параллельных оси Ov c ортом l (рис.2).
Если заранее исключить случай системы, эквивалентной паре сил, нетрудно на основании предыдущего параграфа доказать существование ее равнодействующей R .
Определим координаты центра C (x c , y c , z c ) параллельных сил, то есть координаты точки приложения равнодействующейэтой системы.
Воспользуемся с этой целью теоремой Вариньона, на основании которой:
M 0 (R ) = Σ M 0 (P i ).

Рис.2
Вектор-момент силы можно представить в виде векторного произведения, поэтому:
М 0 (R ) = r c × R = Σ М 0i (P i ) = Σ (r i × P i ).
Учитывая, что R = R v ∙ l , а P i = P vi ∙ l и воспользовавшись свойствами векторного произведения, получим:
r c × R v ∙ l = Σ (r i × P vi ∙ l ),
r c ∙ R v × l = Σ (r i ∙ P vi × l ) = Σ (r i ∙ P vi ) × l ,
или:
[ r c R v - Σ (r i P vi )] × l = 0.
Последнее выражение справедливо только в том случае, если выражение в квадратных скобках равно нулю. Поэтому, опуская индекс v и учитывая, что равнодействующая R = Σ P i , отсюда получим:
r c = (Σ P i r i )/(Σ P i ).
Проектируя последнее векторное равенство на оси координат, получим искомое выражение координат центра параллельных сил :
x c = (Σ P i x i )/(Σ P i );
y c = (Σ P i y i )/(Σ P i );(2)
z c = (Σ P i z i )/(Σ P i ).
Центр тяжести тел.
Координаты центров тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆ V i , то на каждую его часть будет действовать сила притяжения ∆ P i , направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.3), и к ней применимы все выводы предыдущей главы.

Рис.3
Определение . Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
Напомним, что удельным весом элементарной части тела называется отношение ее веса ∆ P i к объему ∆ V i : γ i = ∆ P i / ∆ V i . Для однородного тела эта величина является постоянной: γ i = γ = P / V .
Подставляя в (2) ∆ P i = γ i ∙∆ V i вместо P i , учитывая последнее замечание и сокращая числитель и знаменатель на g , получим выражения координат центра тяжести однородного тела :
x c = (Σ ∆ V i ∙ x i )/(Σ ∆ V i );
y c = (Σ ∆ V i ∙ y i )/(Σ ∆ V i );(3)
z c = (Σ ∆ V i ∙ z i )/(Σ ∆ V i ).
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.
Если оси х и у расположить в этой плоскости симметрии, то для каждой точки с координатами . И координата по (3), будет равна нулю, т.к. в сумме все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Действительно, в этом случае, если ось z провести по оси симметрии, для каждой точки с координатами можно отыскать точку с координатами и координаты и , вычисленные по формулам (3), окажутся равными нулю.
Аналогично доказывается и третья теорема.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
И ещё несколько замечаний.
Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (3) P i – определять как вес соответствующей части и – как координаты её центра тяжести.
Второе. Если тело однородное, то вес отдельной части его , где - удельный вес материала, из которого сделано тело, а V i - объём этой части тела. И формулы (3) примут более удобный вид. Например,
И аналогично, где - объём всего тела.
Третье замечание. Пусть тело имеет вид тонкой пластинки площадью F и толщиной t , лежащей в плоскости Oxy . Подставляя в (3) ∆ V i = t ∙ ∆ F i , получим координаты центра тяжести однородной пластинки :
x c = (Σ ∆ F i ∙ x i ) / (Σ ∆ F i );
y c = (Σ ∆ F i ∙ y i ) / (Σ ∆ F i ).
z c = (Σ ∆ F i ∙ z i ) / (Σ ∆ F i ).
где – координаты центра тяжести отдельных пластин; – общая площадь тела.
Четвёртое замечание. Для тела в виде тонкого криволинейного стержня длиной L с площадью поперечного сечения a элементарный объем ∆ V i = a ∙∆ L i , поэтому координаты центра тяжести тонкого криволинейного стержня будут равны:
x c = (Σ ∆ L i ∙ x i )/(Σ ∆ L i );
y c = (Σ ∆ L i ∙ y i )/(Σ ∆ L i );(4)
z c = (Σ ∆ L i ∙ z i )/(Σ ∆ L i ).
где – координаты центра тяжести i -го участка; .
Отметим, что согласно определению центр тяжести - это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).
Примечание.
В этом разделе курса мы не делаем разницы между силой притяжения, силой тяжести и весом тела. В действительности сила тяжести представляет собой разность между силой притяжения Земли и центробежной силой, вызванной ее вращением.
Координаты центров тяжести неоднородных тел.
Координаты центра тяжести неоднородного твердого тела (рис.4) в выбранной системе отсчета определяются следующим образом:

Рис.4

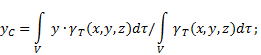

где - вес единицы объема тела (удельный вес)
![]() -вес всего тела.
-вес всего тела.
неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.5
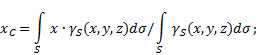

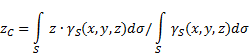
где - вес единицыплощади тела,
![]() -вес всего тела.
-вес всего тела.
Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.6

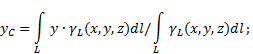

где - вес единицыдлины тела,
Вес всего тела.
Способы определения координат центра тяжести.
Исходя из полученных выше общих формул,можно указать конкретные способы определения координат центров тяжести тел .
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.7
2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.
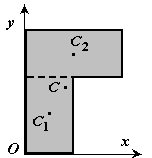
Рис.8
S =S 1 +S 2 .
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки(без выреза) с площадью S 1 и площади вырезанной части S 2 .

Рис.9
S = S 1 - S 2 .
4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.
Центры тяжести некоторых однородных тел.
1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).

Рис.10
Найдем координату по формуле . Для этого выделим на дуге АВ элемент ММ ’ длиною , положение которого определяется углом . Координата х элемента ММ’ будет . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
![]()
где L - длина дуги АВ , равная .
Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О , равном
где угол измеряется в радианах.
2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy , координаты вершин которого известны: A i (x i ,y i ), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А 1 А 2 , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А 3 М 3 (рис.11) .

Рис.11
Разбивая треугольник на полоски, параллельные стороне А 2 А 3 , можно убедиться, что он должен лежать на медиане А 1 М 1 . Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан , которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.
В частности, для медианы А 1 М 1 получим, учитывая, что координаты точки М 1 - это среднее арифметическое координат вершин А 2 иА 3 :
x c = x 1 + (2/3) ∙ (x М 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:
x c =(1/3) Σ x i ; y c =(1/3) Σ y i .
3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2 α , расположенный симметрично относительно оси Ox (рис.12) .
Очевидно, что y c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:


Рис.12
Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом d φ . С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R × d φ и высотой R . Площадь такого треугольника dF =(1/2)R 2 ∙ d φ , а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R ∙ cosφ . Подставляя в (5) F = α R 2 , получим:

С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга .
Подставляя в (2) α = π /2, получим: x c = (4 R )/(3 π ) ≅ 0,4 R .
Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.

Рис.13
Решение. Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
Объёмы их:
Поэтому координаты центра тяжести тела
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

Рис.14
Решение. Координаты центров тяжести:
0.
Площади:
Поэтому:
Пример 3.
У квадратного листа
см вырезано
квадратное отверстие
см (рис.15).
Найдем центр тяжести листа.
Пример 4.
Найти
положение центра тяжести пластинки, представленной на рис. 16. Размеры даны в
сантиметрах.

Рис.16
Решение. Разделим пластинку на фигуры (рис. 17), центры тяжести которых известны.
Площади этих фигур и координаты их центров тяжести:
1) прямоугольник со сторонами 30 и 40 см, S 1 =30 ∙ 40=1200 см 2 ; х 1 =15 см; у 1 =20 см.
2) прямоугольный треугольник с основанием 50 см и высотой 40 см; S 2 =0,5 ∙ 50 ∙ 40= 1000 см 2 ; х 2 =30+50/3=46,7 см;у 2 = 40/3 =13,3 см;
3) половина круга окружности радиуса r = 20 см; S 3 =0,5 ∙π∙ 20 2 =628 см 2 ; х 3 =4 R /3 π =8,5 см; у
Решение. Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ = ρ g , где g - ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

Рис.19
Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.
Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:
где L i длина i -го стержня фермы, а x i , y i - координаты его центра тяжести.
Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.
Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.
Первая группа состоит из первого стержня,для нее L 1 = 4 м, x 1 = 0 м, y 1 = 2 м. Вторая группа стержней состоит из пяти стержней, для нее L 2 = 20 м, x 2 = 3 м, y 2 = 2 м.
Координаты центра тяжести фермы находим по формуле:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 м;
y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 м.
Отметим, что центр С лежит на прямой, соединяющей С 1 и С 2 и делит отрезок С 1 С 2 в отношении: С 1 С /СС 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Вопросы для самопроверки
- Что называется центром параллельных сил?
- Как определяются координаты центра параллельных сил?
- Как определить центр параллельных сил, равнодействующая которых равна нулю?
- Каким свойством обладает центр параллельных сил?
- По каким формулам вычисляются координаты центра параллельных сил?
- Что называется центром тяжести тела?
- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?
- Что называют статическим моментом площади?
- Приведите пример тела, центр тяжести которого расположен вне тела.
- Как используются свойства симметрии при определении центров тяжести тел?
- В чем состоит сущность способа отрицательных весов?
- Где расположен центр тяжести дуги окружности?
- Каким графическим построением можно найти центр тяжести треугольника?
- Запишите формулу, определяющую центр тяжести кругового сектора.
- Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.
- По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?
- Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?
- Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?
- Какими вспомогательными теоремами пользуются при определении положения центра тяжести?
Умение оставаться в равновесии не прилагая к этому усилий очень важно для эффективной медитации, занятий йогой, цигун и так же для танцев живота. Это первое требование, скоторым, сталкиваются новички в этих видах занятий и одна из причин, по которым трудно сделать первые шаги без инструктора. Вопрос подсказывающий о том что человек своего центра тяжести не знает может выглядеть несколько по разному. В цигун, например, человек спросит как быть расслабленным и при этом выполнять движения стоя, начинающая танцовщица восточных танцев не будет понимать как разделить и координировать движения нижних и верхних частей туловища, а так же в обеих случаях люди будут перенапрягаться и часто терять устойчивость. Движения их будут неуверенными, неуклюжими.
По этому, важно понять как найти свой центр тяжести самому, это требует как мыслительной работы, так и сноровки, но со временем навык переходит на инстинктивный уровень.
Что нужно сделать чтобы не напрягать мышцы и при этом не пользоваться внешними опорами. Ответ очевиден, нужно перенести опору внутрь. Точнее опереться на условную внутреннюю ось. Где эта ось проходит? Понятие центра тяжести условное, но тем не менее применяется в физике. Там ее принято определять как точку приложения равнодействующей сил тяжести. Равнодействующая сила тяжести это совокупность всех сил тяжести с учетом направления их действия.
Сложновато пока? Запаситесь терпением.
То есть, мы ведь ищем точку в своем теле которая позволит нам не падать, не борясь при этом сознательно с земным притяжением. Это значит, что сила тяжести земли должна быть направленна так, чтобы она сходилась с остальными действующими силами где-то в центре нашего тела.

Такое направление сил создает условную ось в самом центре нашего тела, вертикальную поверхности это и есть вертикаль центра тяжести. Та часть тела которой мы упираемся в землю является нашей площадью опоры (мы упираемся в землю ступнями) В месте где эта вертикаль упирается в поверхность на которой мы стоим, то есть упираемся в землю, это точка центра тяжести внутри площади опоры. Если вертикаль сместиться из этого места, мы равновесие потеряем и упадем. Чем больше сама площадь опоры, тем нам легче оставаться близко к ее центру, и потому мы все инстинктивно будем делать широкий шаг стоя на не устойчивой поверхности. То есть площадь опоры это не только сами ступни, но еще и пространство между ними.

Еще важно знать что ширина площади опоры влияет сильнее чем длина. В случае человека, это значит что у нас больше шансов упасть на бок чем назад и уж тем более вперед. По этому при беге нам тяжелее удерживать равновесие, то же самое можно сказать о каблуках. А вот в широкой устойчивой обуви, устоять наоборот легче, даже легче чем совсем уж босяком. Однако упомянутые в начале виды активности предполагают очень мягкую, легкую обувь или ее полное отсутствие. По этому, помогать себе обувью мы не сможем.

Значит, очень важно найти центральную точку вертикальной линии на своей ступне. Обычно она располагается не в центре ступни, как некоторые автоматически предполагают, а ближе к пятке, где то на пол пути от центра ступни, к пятке.
Но это еще не все.
Кроме вертикальной линии центра тяжести есть еще горизонтальная, а так же отдельная для конечностей.
Горизонтальная линия у женщин и мужчин проходит немного по разному.
Впереди у женщин она проходит ниже, а у мужчин выше. У мужчин она проходит где-то на 4-5 пальцев ниже пупка, а у женщин на 10, примерно. Сзади женская линия проходит почти укопчика, а мужская выше него примерно на пять пальцев. Кроме того, для устойчивости в момент медитации важно обратить внимание на отвесную линию центра тяжести колена. Онарасположена немного выше кости (голени), но на два или три пальца ниже хряща.
Во время медитаций, как и во время танца живота, расставлять широко ступни не очень хорошо, максимальная ширина, обычно соответствует ширине плеч.
По этому, нужно немного помочь себе коленями попытавшись выстроить вертикальную ось как можно прямее. Станьте перед зеркалом, найдите на себе все описанные точки. Ногипоставьте на ширине плеч. Расслабьте мышцы ног и тела. Затем, выпрямите спину, не напрягая тело, расслабьте ноги немного согнув колени. Представьте себе три вертикальных линии, каждая из которых проходит в соответствующей точке в задней части туловища, в передней его части и в районе колен. Попытайтесь расположить точки так, чтобы передняя ось туловища была примерно на полпути меж задней и коленной осью. При этом колени не следует загибать так, чтобы они заходили за носок, они должны быть лишь немного согнуты и хорошо расслаблены. Желательно над центром тяжести внутри площади опоры, который мы нашли на ступне. Руки при этом можно свободно расположить по богам либо положить ладони на бедра.

Как вы будете знать, что нашли свой центр тяжести?
Вы будете ощущать легкое покачивание, но при этом точно будете знать, что не упадете.
Цель работы – определить центр тяжести сложной фигуры аналитическим и опытным путями.
Теоретическое обоснование. Материальные тела состоят из элементарных частиц, положение которых в пространстве определяется их координатами. Силы притяжения каждой частицы к Земле можно считать системой параллельных сил, равнодействующая этих сил называется силой тяжести тела или весом тела. Центр тяжести тела – это точка приложения силы тяжести.
Центр тяжести – это геометрическая точка, которая может быть расположена и вне тела (например, диск с отверстием, полый шар и т.п.). Большое практическое значение имеет определение центра тяжести тонких плоских однородных пластин. Их толщиной обычно можно пренебречь и считать, что центр тяжести расположен в плоскости. Если координатную плоскость xOy совместить с плоскостью фигуры, то положение центра тяжести определяется двумя координатами:
где - площадь части фигуры, ();
– координаты центра тяжести частей фигуры, мм (см).
| Сечение фигуры | А, мм 2 | X c ,мм | Y c , мм |
 | bh | b/2 | h/2 |
 | bh/2 | b/3 | h/3 |
 | R 2 a | ||
| При 2α = π πR 2 /2 |
Порядок проведения работы .
Начертить фигуру сложной формы, состоящую из 3-4 простых фигур (прямоугольник, треугольник, круг и т.п.) в масштабе 1:1 и проставить ее размеры.
Провести оси координат так, чтобы они охватывали всю фигуру, разбить сложную фигуру на простые части, определить площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат.
Вычислить координаты центра тяжести всей фигуры аналитически. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить два отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.
Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в другой точке. Центр тяжести фигуры, найденный опытным путем, должны совпадать.
Определить координаты центра тяжести тонкой однородной пластины аналитически. Проверку произвести опытным путем
Алгоритм решения
1. Аналитический способ.
а) Чертеж вычертить в масштабе 1:1.
б) Сложную фигуру разбить на простые
в) Выбрать и провести оси координат (если фигура симметричная, то – по оси симметрии, в противном случае – по контору фигуры)
г) Вычислить площадь простых фигур и всей фигуры
д) Отметить положение центра тяжести каждой простой фигуры на чертеже
е) Вычислить координаты центра тяжести каждой фигуры
(по оси x и y)
ж) Вычислить координаты центра тяжести всей фигуры по формуле
з) Отметить положение центра тяжести на чертеже С (
2. Опытное определение.
Правильность решения задачи проверить опытным путем. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить три отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.
Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в других точках. Значение координат центра тяжести фигуры, найденных при подвешивании фигуры в двух точках: . Центр тяжести фигуры, найденный опытным путем, должны совпадать.
3.Заключение о положении центра тяжести при аналитическом и опытном определении.
Задание
Определить центр тяжести плоского сечения аналитическим и опытным путем.
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Пример выполнения
Задача
Определить координаты центра тяжести тонкой однородной пластины.

I Аналитический способ
1. Чертеж вычерчивается в масштабе (размеры обычно даны в мм)
2. Сложную фигуру разбиваем на простые.
1- Прямоугольник
2- Треугольник (прямоугольник)
3- Площадь полуокружности (ее нет, знак минус).
Находим положение центра тяжести простых фигур точек , и

3. Проводим оси координат как удобно и отмечаем начало координат т. О.
4. Вычисляем площади простых фигур и площадь всей фигуры. [размер в см]
(3. нет, знак -).
Площадь всей фигуры
5. Находим координату ц.т. , и на чертеже.
6. Вычисляем координаты точек C 1 , C 2 и C 3
7. Вычисляем координаты точки C
8. На чертеже отмечаем точку
II Опытным путем

Координаты центра тяжести опытным путем .
Контрольные вопросы.
1. Можно ли рассматривать силу тяжести тела как равнодействующую систему параллельных сил?
2. Может ли располагаться центр тяжести все самого тела?
3. В чем сущность опытного определения центра тяжести плоской фигуры?
4. Как определяется центр тяжести сложной фигуры, состоящей из нескольких простых фигур?
5. Как следует рационально производить разбиение фигуры сложной формы на простые фигуры при определении центра тяжести всей фигуры?
6. Какой знак имеет площадь отверстий в формуле для определения центра тяжести?
7. На пересечении каких линий треугольника находится его центр тяжести?
8. Если фигуру трудно разбить на небольшое число простых фигур, какой способ определения центра тяжести может дать наиболее быстрый ответ?
Практическая работа №6
«Решение задач комплексного характера»
Цель работы: уметь решать задачи комплексного характера (кинематика, динамика)
Теоретическое обоснование: Скорость есть кинематическая мера движения точки, характеризующая быстроту изменения ее положения. Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени. При задании движения точки уравнениями проекции скорости на оси декартовых координат равны:
Модуль скорости точки определяется по формуле
Направление скорости определяется направляющими косинусами:

Характеристикой быстроты изменения скорости является ускорение а. Ускорение точки равно производной от вектора скорости по времени:
При задании движения точки уравнения проекции ускорения на координатные оси равны:

Модуль ускорения:

Модуль полного ускорения
Модуль касательного ускорения определяется по формуле

Модуль нормального ускорения определяется по формуле
где – радиус кривизны траектории в данной точке.
Направление ускорения определяется направляющими косинусами

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид
Угловая скорость тела:
Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой . Зависимость между и имеет вид
Угловое ускорение тела:

Сила, равная произведению массы данной точке на ее ускорение и направление в сторону прямопротивоположную ускорению точки, называется силой инерции.
Мощностью называется работа, выполненная силой в единицу времени
Основное уравнение динамики для вращательного движения
– момент инерции тела относительно оси вращения, есть сумма произведений масс материальных точек на квадрат расстояний их до этой оси
Задание
Тело массой m с помощью троса, наматываемого на барабан диаметром d, перемещается вверх или вниз по наклонной плоскости с углом наклона α. Уравнение движения тела S=f(t), уравнение вращения барабана , где S в метрах; φ - в радианах; t – в секундах. P и ω - соответственно мощность и угловая скорость на валу барабана в момент конца разгона или начала торможения. Время t 1 – время разгона (из состояния покоя до заданной скорости) или торможения (от заданной скорости до остановки). Коэффициент трения скольжения между телом и плоскостью –f. Потерями на трение на барабане, а также массой барабана пренебречь. При решении задач принять g=10 м/с 2
| № вар | α, град | Закон движения | Напр движ | m, кг | t 1 , c | d, м | P, кВт | , рад/с | f | Опред. величины |
| S=0,8t 2 | Вниз | - | - | 0,20 | 4,0 | 0,20 | m,t 1 | |||
| φ=4t 2 | Вниз | 1,0 | 0,30 | - | - | 0,16 | P,ω | |||
| S=1,5t-t 2 | вверх | - | - | - | 4,5 | 0,20 | m, d | |||
| ω=15t-15t 2 | вверх | - | - | 0,20 | 3,0 | - | 0,14 | m,ω | ||
| S=0,5t 2 | Вниз | - | - | 1,76 | 0,20 | d,t 1 | ||||
| S=1,5t 2 | Вниз | - | 0,6 | 0,24 | 9,9 | - | 0,10 | m,ω | ||
| S=0,9t 2 | Вниз | - | 0,18 | - | 0,20 | P, t 1 | ||||
| φ=10t 2 | Вниз | - | 0,20 | 1,92 | - | 0,20 | P, t 1 | |||
| S=t-1,25t 2 | вверх | - | - | - | 0,25 | P,d | ||||
| φ=8t-20t 2 | вверх | - | 0,20 | - | - | 0,14 | P, ω |
Пример выполнения
Задача 1 (рисунок 1).
Решение 1. Прямолинейное движение (рисунок 1, а). Точка, двигавшаяся равномерно, в некоторый момент времени получила новый закон движения , и через некоторый промежуток времени остановилась. Определить все кинематические характеристики движения точки для двух случаев; а) движение по прямолинейной траектории; б) движение по криволинейной траектории постоянного радиуса кривизны r=100см
Рисунок 1 (а).
Закон изменения скорости точки
Начальную скорость точки найдем из условия:
Время торможения до остановки найдем из условия:
при , отсюда .
Закон движения точки в период равномерного движения
Расстояние, пройденное точкой по траектории за период торможения,
Закон изменения касательного ускорения точки
откуда следует, что в период торможения точка двигалась равнозамедленно, так как касательное ускорение отрицательно и по значению постоянно.
Нормальное ускорение точки на прямолинейной траектории движения равно нулю, т.е. .
Решение 2. Криволинейное движение (рисунок 1, б).
Рисунок 1 (б)

В этом случае по сравнению со случаем прямолинейного движения остаются без изменения все кинематические характеристики, за исключением нормального ускорения.
Закон изменения нормального ускорения точки
Нормальное ускорение точки в начальный момент торможения
Принятая на чертеже нумерация положений точки на траектории: 1 – текущее положение точки в равномерном движении до начала торможения; 2 – положение точки в момент начала торможения; 3 – текущее положение точки в период торможения; 4 – конечное положение точки.
Задача 2.
Груз (рис. 2, а) поднимается с помощью барабанной лебедки. Диаметр барабана d=0,3м, а закон его вращения .
Разгон барабана длился до угловой скорости . Определить все кинематические характеристики движения барабана и груза.


Решение . Закон изменения угловой скорости барабана . Начальную угловую скорость найдем из условия: ; следовательно, разгон начался из состояния покоя. Время разгона найдем из условия: . Угол поворота барабана за период разгона .
Закон изменения углового ускорения барабана , отсюда следует, что в период разгона барабан вращался равноускоренно.
Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки A, лежащей на ободе барабана (рис. 2, б). Как известно, линейные характеристики точки вращающегося тела определяются через его угловые характеристики.
Расстояние, пройденное грузом за период разгона, . Скорость груза в конце разгона .
Ускорение груза .
Закон движения груза .
Расстояние, скорость и ускорение груза можно было определить и иначе, через найденный закон движения груза:
Задача 3.
Груз, перемещавшийся равномерно вверх по наклонной опорной плоскости, в некоторый момент времени получил торможение в соответствии с новым законом движения ![]() , где s – в метрах и t – в секундах. Масса груза m = 100кг, коэффициент трения скольжения между грузом и плоскостью f=0,25. Определить силу F и мощность на тяговом тросе для двух моментов времени: а) равномерное движение до начала торможения;
, где s – в метрах и t – в секундах. Масса груза m = 100кг, коэффициент трения скольжения между грузом и плоскостью f=0,25. Определить силу F и мощность на тяговом тросе для двух моментов времени: а) равномерное движение до начала торможения;
б) начальный момент торможения. При расчёте принять g=10 м/ .
Решение. Определяем кинематические характеристики движения груза.
Закон изменения скорости груза
Начальная скорость груза (при t=0)
Ускорение груза
Так как ускорение отрицательно, то движение – замедленное.
1. Равномерное движение груза.

Для определения движущей силы F рассматриваем равновесие груза, на который действует система сходящихся сил: сила на тросе F, сила тяжести груза G=mg, нормальная реакция опорной поверхности N и сила трения , направленная навстречу движению тела. По закону трения, . Выбираем направление координатных осей, как показано на чертеже, и составляем два уравнения равновесия для груза:
Мощность на тросе до начала торможения определим по известной формуле
Где м/с.
2. Замедленное движение груза.

Как известно, при неравномерном поступательном движении тела система действующих на него сил по направлению движения не является уравновешенной. Согласно принципу Даламбера (метод кинетостатики), тело в этом случае можно считать находящимся в условном равновесии, если ко всем действующим на него силам добавить силу инерции , вектор которой направлен противоположно вектору ускорения. Вектор ускорения в нашем случае направлен противоположно вектору скорости, так как груз движется замедленно. Составляем два уравнения равновесия для груза:
Мощность на тросе в момент начала торможения
Контрольные вопросы.
1. Как определить численное значение и направление скорости точки в данный момент?
2. Что характеризует нормальная и касательная составляющие полного ускорения?
3. Как перейти от выражения угловой скорости в мин -1 к ее выражению рад/с?
4. Что называют массой тела? Назовите единицу измерения массы
5. При каком движении материальной точки возникает сила инерции? Чему равно ее численное значение, как она направлена?
6. Сформулируйте принцип Даламбера
7. Возникает ли сила инерции при равномерном криволинейном движении материальной точки?
8. Что такое вращающий момент?
9. Как выражается зависимость между вращающим моментом и угловой скорости при данной передаваемой мощности?
10. Основное уравнение динамики для вращательного движения.
Практическая работа №7
«Расчет конструкций на прочность»
Цель работы: определять прочность, размеры сечения и допускаемую нагрузку
Теоретическое обоснование.
Зная силовые факторы и геометрические характеристики сечения при деформации растяжение (сжатие), мы можем определить напряжение по формулам. А что бы понять, выдержит ли наша деталь (вал, шестерня и т. д.) внешнюю нагрузку. Необходимо эту величину сравнить с допустимым напряжением.
Итак, уравнение статической прочности
На его основании решают 3 типа задач:
1) проверка прочности
2) определение размеров сечения
3) определение допускаемой нагрузки
Итак, уравнение статической жёсткости
На его основании решают также 3 типа задач
Уравнение статической прочности при растяжении (сжатии)
![]()
1) Первый тип - проверка прочности
![]() ,
,
т. е. решаем левую часть и сравниваем с допускаемым напряжением.
2) Второй тип - определение размеров сечения
![]()
из правой части площадь поперечного сечения
 Сечение круг
Сечение круг
отсюда диаметр d
Сечение прямоугольник

Сечение квадрат

A = a² (мм²)
Сечение полукруг

Сечения швеллер, двутавр, уголок и т. д.
Значения площади - из таблицы, принимается по ГОСТ
3) Третий тип - определение допустимой нагрузки;
![]()
принимается в меньшую сторону, целое число
ЗАДАНИЕ
Задача
А) Проверка прочности (проверочный расчет)
Для заданного бруса построить эпюру продольных сил и проверить прочность на обоих участках. Для материала бруса (сталь Ст3) принять ![]()
![]()
| № варианта | ||||||
| 12,5 | 5,3 | - | - | |||
| 2,3 | - | - | ||||
| 4,2 | - | - |
Б) Подбор сечения (проектный расчет)
Для заданного бруса построить эпюру продольных сил и определить размеры поперечного сечения на обоих участках. Для материала бруса (сталь Ст3) принять
| № варианта | ||
| 1,9 | 2,5 | |
| 2,8 | 1,9 | |
| 3,2 |
В) Определение допускаемой продольной силы
Для заданного бруса определить допускаемые значения нагрузок и ,
построить эпюру продольных сил. Для материала бруса (сталь Ст3) принять . При решении задачи считать, что на обоих участках бруса вид нагружения одинаков.
| № варианта | ||||
| - | - | |||
| - | - | |||
| - | - |

 Пример выполнения задания
Пример выполнения задания
Задача 1 (рисунок 1).
Проверить прочность колонны, выполненной из двутавровых профилей заданного размера. Для материала колонны (сталь Ст3) принять допускаемые напряжения при растяжении ![]() и при сжатии
и при сжатии ![]() . В случае наличия перезагрузки или значительной недогрузки подобрать размеры двутавров, обеспечивающие оптимальную прочность колонны.
. В случае наличия перезагрузки или значительной недогрузки подобрать размеры двутавров, обеспечивающие оптимальную прочность колонны.
Решение.
Заданный брус имеет два участка 1, 2. Границами участков являются сечения, в которых приложены внешние силы. Так как силы, нагружающие брус, расположены по его центральной продольной оси, то в поперечных сечениях возникает лишь один внутренний силовой фактор – продольная сила , т.е. имеет место растяжение (сжатие) бруса.

Для определения продольной силы применяем метод сечений метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать нижнюю закрепленную часть бруса и оставлять для рассмотрения верхнюю часть. На участке 1 продольная сила постоянна и равна
Знак минус указывает на то, что на обоих участках брус сжат.
Строим эпюру продольных сил . Проведя параллельно оси бруса базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения . Как видим, эпюра оказалась очерчена прямыми линиями, параллельными базовой.
Выполняем проверку прочности бруса, т.е. определяем расчетное напряжение (для каждого участка в отдельности) и сравниваем его с допускаемым. Для этого используем условие прочности при сжатии
![]()
где площадь является геометрической характеристикой прочности поперечного сечения. Из таблицы прокатной стали берем:
для двутавра
для двутавра
Проверка прочности:
Значения продольных сил взяты по абсолютной величине.
Прочность бруса обеспечена, однако имеет место значительная (более 25%) недогрузка, что недопустимо вследствие перерасхода материала.
Из условия прочности определяем новые размеры двутавра для каждого из участков бруса:
Отсюда требуемая площадь
По таблице ГОСТа выбираем двутавр № 16 , для которого ;
Отсюда требуемая площадь
По таблице ГОСТа выбираем двутавр №24, для которого ;
При выбранных размерах двутавров также имеет место недогрузка, однако незначительная (менее 5%)
Задача №2.
Для бруса с заданными размерами поперечного сечения определить допускаемые значения нагрузок и . Для материала бруса (сталь Ст3) принять допускаемые напряжения при растяжении ![]() и при сжатии
и при сжатии ![]() .
.

Решение.
Заданный брус имеет два участка 1, 2. Имеет место растяжение (сжатие) бруса.
Применяя метод сечений, определяем продольную силу , выражая ее через искомые силы и . Проводя в пределах каждого из участков сечение, будем отбрасывать левую часть бруса и оставлять для рассмотрения правую часть. На участке 1 продольная сила постоянна и равна
На участке 2 продольная сила также постоянна и равна
Знак плюс указывает на то, что на обоих участкахбрус растянут.
Строим эпюру продольных сил . Эпюра очерчена прямыми линиями, параллельными базовой.

Из условия прочности при растяжении определяем допускаемые значения нагрузок и предварительно вычислив площади заданных поперечных сечений:
![]()
![]()
Контрольные вопросы.
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Запишите условие прочности при растяжении и сжатии.
3. Как назначают знаки продольной силы и нормального напряжения?
4. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
5. Различаются ли условия прочности при расчете на растяжение и расчете на сжатие?
6. В каких единицах измеряется напряжение?
7. Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?
8. В чем разница между предельным и допускаемым напряжением?
Практическая работа №8
«Решение задач по определению главных центральных моментов инерции плоских геометрических фигур»
Цель работы: определить аналитическим путем моменты инерции плоских тел сложной формы
Теоретическое обоснование. Координаты центра тяжести сечения можно выразить через статический момент:
![]()
где относительно оси Оx
относительно оси Оy
Статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние ее центра тяжести до этой оси. Статический момент имеет размерность . Статический момент может быть величиной положительной, отрицательной и равен нулю (относительно любой центральной оси).
Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения
Осевой момент инерции выражается в единицах - . Осевой момент инерции- величина всегда положительная и не равна нулю.
Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.
Момент инерции относительно какой-либо оси равен центра
Нарисуйте схему системы и отметьте на ней центр тяжести. Если найденный центр тяжести находится вне системы объектов, вы получили неверный ответ. Возможно, вы измерили расстояния от разных точек отсчета. Повторите измерения.
- Например, если на качелях сидят дети, центр тяжести будет где-то между детьми, а не справа или слева от качелей. Также центр тяжести никогда не совпадет с точкой, где сидит ребенок.
- Эти рассуждения верны в двумерном пространстве. Нарисуйте квадрат, в котором поместятся все объекты системы. Центр тяжести должен находиться внутри этого квадрата.
Проверьте математические вычисления, если вы получили маленький результат. Если точка отсчета находится на одном конце системы, маленький результат помещает центр тяжести возле конца системы. Возможно, это правильный ответ, но в подавляющем большинстве случаев такой результат указывает на ошибку. Когда вы вычисляли моменты, вы перемножали соответствующие веса и расстояния? Если вместо умножения вы сложили веса и расстояния, вы получите гораздо меньший результат.
Исправьте ошибку, если вы нашли несколько центров тяжести. Каждая система имеет только один центр тяжести. Если вы нашли несколько центров тяжести, скорее всего, вы не сложили все моменты. Центр тяжести равен отношению «суммарного» момента к «суммарному» весу. Не нужно делить «каждый» момент на «каждый» вес: так вы найдете положение каждого объекта.
Проверьте точку отсчета, если ответ отличается на некоторое целое значение. В нашем примере ответ равен 3,4 м. Допустим, вы получили ответ 0,4 м или 1,4 м, или другое число, оканчивающееся на «,4». Это потому, что в качестве точки отсчета вы выбрали не левый конец доски, а точку, которая расположена правее на целую величину. На самом деле, ваш ответ верен, независимо от того, какую точку отсчета вы выбрали! Просто запомните: точка отсчета всегда находится в положении x = 0. Вот пример:
- В нашем примере точка отсчета находилась на левом конце доски и мы нашли, что центр тяжести находится на расстоянии 3,4 м от этой точки отсчета.
- Если в качестве точки отсчета выбрать точку, которая расположена на расстоянии 1 м вправо от левого конца доски, вы получите ответ 2,4 м. То есть центр тяжести находится на расстоянии 2,4 м от новой точки отсчета, которая, в свою очередь, находится на расстоянии 1 м от левого конца доски. Таким образом, центр тяжести находится на расстоянии 2,4 + 1 = 3,4 м от левого конца доски. Получился старый ответ!
- Примечание: при измерении расстояния помните, что расстояния до «левой» точки отсчета отрицательные, а до «правой» – положительные.
Расстояния измеряйте по прямым линиям. Предположим, на качелях два ребенка, но один ребенок намного выше другого, или один ребенок висит под доской, а не сидит на ней. Проигнорируйте такую разницу и измерьте расстояния по прямой линии доски. Измерение расстояний под углами приведет к близким, но не совсем точным результатам.
- В случае задачи с качелями-доской помните, что центр тяжести находится между правым и левым концами доски. Позже вы научитесь вычислять центр тяжести более сложных двумерных систем.



